| .. | ||
| doc | ||
| bignumber.d.ts | ||
| bignumber.js | ||
| bignumber.js.map | ||
| bignumber.min.js | ||
| bignumber.mjs | ||
| bower.json | ||
| CHANGELOG.md | ||
| LICENCE | ||
| package.json | ||
| README.md | ||
A JavaScript library for arbitrary-precision decimal and non-decimal arithmetic.
Features
- Integers and decimals
- Simple API but full-featured
- Faster, smaller, and perhaps easier to use than JavaScript versions of Java's BigDecimal
- 8 KB minified and gzipped
- Replicates the
toExponential,toFixed,toPrecisionandtoStringmethods of JavaScript's Number type - Includes a
toFractionand a correctly-roundedsquareRootmethod - Supports cryptographically-secure pseudo-random number generation
- No dependencies
- Wide platform compatibility: uses JavaScript 1.5 (ECMAScript 3) features only
- Comprehensive documentation and test set
If a smaller and simpler library is required see big.js.
It's less than half the size but only works with decimal numbers and only has half the methods.
It also does not allow NaN or Infinity, or have the configuration options of this library.
See also decimal.js, which among other things adds support for non-integer powers, and performs all operations to a specified number of significant digits.
Load
The library is the single JavaScript file bignumber.js (or minified, bignumber.min.js).
Browser:
<script src='path/to/bignumber.js'></script>
$ npm install --save bignumber.js
var BigNumber = require('bignumber.js');
ES6 module (bignumber.mjs):
//import BigNumber from 'bignumber.js';
import {BigNumber} from 'bignumber.js';
AMD loader libraries such as requireJS:
require(['bignumber'], function(BigNumber) {
// Use BigNumber here in local scope. No global BigNumber.
});
Use
In all examples below, var, semicolons and toString calls are not shown.
If a commented-out value is in quotes it means toString has been called on the preceding expression.
The library exports a single function: BigNumber, the constructor of BigNumber instances.
It accepts a value of type Number, String or BigNumber,
x = new BigNumber(123.4567)
y = BigNumber('123456.7e-3')
z = new BigNumber(x)
x.isEqualTo(y) && y.isEqualTo(z) && x.isEqualTo(z) // true
and a base can be specified.
a = new BigNumber(1011, 2) // "11"
b = new BigNumber('zz.9', 36) // "1295.25"
c = x.plus(y) // "1306.25"
Note that a BigNumber is created from a Number's decimal toString() value not from its underlying binary value. If the latter is required, then pass the Number's toString(2) value and specify base 2.
new BigNumber(Number.MAX_VALUE.toString(2), 2)
If the limited precision of Number values is not well understood, it is recommended to pass String values rather than Number values to avoid a potential loss of precision.
// Precision loss from using numeric literals with more than 15 significant digits.
new BigNumber(1.0000000000000001); // '1'
new BigNumber(88259496234518.57); // '88259496234518.56'
new BigNumber(99999999999999999999); // '100000000000000000000'
// Precision loss from using numeric literals outside the range of Number values.
new BigNumber(2e+308); // 'Infinity'
new BigNumber(1e-324); // '0'
// Precision loss from the unexpected result of arithmetic with Number values.
new BigNumber(0.7 + 0.1); // '0.7999999999999999'
A BigNumber is immutable in the sense that it is not changed by its methods.
0.3 - 0.1 // 0.19999999999999998
x = new BigNumber(0.3)
x.minus(0.1) // "0.2"
x // "0.3"
The methods that return a BigNumber can be chained.
x.dividedBy(y).plus(z).times(9)
x.times('1.23456780123456789e+9').plus(9876.5432321).dividedBy('4444562598.111772').integerValue()
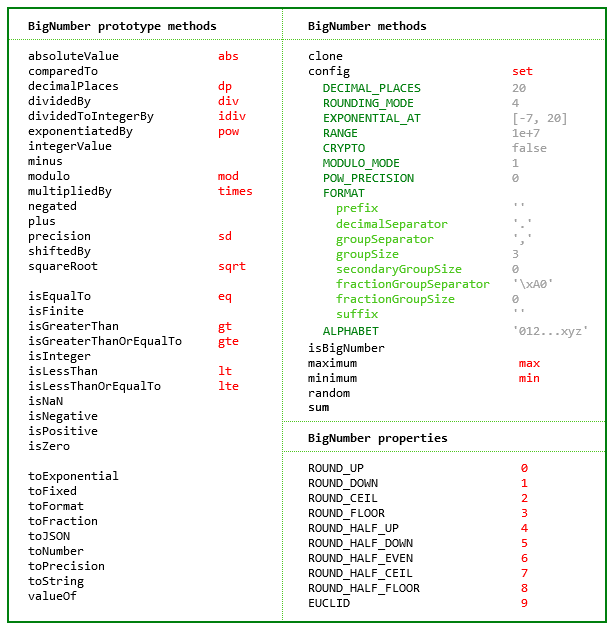
Some of the longer method names have a shorter alias.
x.squareRoot().dividedBy(y).exponentiatedBy(3).isEqualTo( x.sqrt().div(y).pow(3) ) // true
x.modulo(y).multipliedBy(z).eq( x.mod(y).times(z) ) // true
As with JavaScript's Number type, there are toExponential, toFixed and toPrecision methods
x = new BigNumber(255.5)
x.toExponential(5) // "2.55500e+2"
x.toFixed(5) // "255.50000"
x.toPrecision(5) // "255.50"
x.toNumber() // 255.5
and a base can be specified for toString.
x.toString(16) // "ff.8"
There is also a toFormat method which may be useful for internationalisation
y = new BigNumber('1234567.898765')
y.toFormat(2) // "1,234,567.90"
The maximum number of decimal places of the result of an operation involving division (i.e. a division, square root, base conversion or negative power operation) is set using the config method of the BigNumber constructor.
The other arithmetic operations always give the exact result.
BigNumber.config({ DECIMAL_PLACES: 10, ROUNDING_MODE: 4 })
x = new BigNumber(2);
y = new BigNumber(3);
z = x.dividedBy(y) // "0.6666666667"
z.squareRoot() // "0.8164965809"
z.exponentiatedBy(-3) // "3.3749999995"
z.toString(2) // "0.1010101011"
z.multipliedBy(z) // "0.44444444448888888889"
z.multipliedBy(z).decimalPlaces(10) // "0.4444444445"
There is a toFraction method with an optional maximum denominator argument
y = new BigNumber(355)
pi = y.dividedBy(113) // "3.1415929204"
pi.toFraction() // [ "7853982301", "2500000000" ]
pi.toFraction(1000) // [ "355", "113" ]
and isNaN and isFinite methods, as NaN and Infinity are valid BigNumber values.
x = new BigNumber(NaN) // "NaN"
y = new BigNumber(Infinity) // "Infinity"
x.isNaN() && !y.isNaN() && !x.isFinite() && !y.isFinite() // true
The value of a BigNumber is stored in a decimal floating point format in terms of a coefficient, exponent and sign.
x = new BigNumber(-123.456);
x.c // [ 123, 45600000000000 ] coefficient (i.e. significand)
x.e // 2 exponent
x.s // -1 sign
For advanced usage, multiple BigNumber constructors can be created, each with their own independent configuration which applies to all BigNumber's created from it.
// Set DECIMAL_PLACES for the original BigNumber constructor
BigNumber.config({ DECIMAL_PLACES: 10 })
// Create another BigNumber constructor, optionally passing in a configuration object
BN = BigNumber.clone({ DECIMAL_PLACES: 5 })
x = new BigNumber(1)
y = new BN(1)
x.div(3) // '0.3333333333'
y.div(3) // '0.33333'
For futher information see the API reference in the doc directory.
Test
The test/modules directory contains the test scripts for each method.
The tests can be run with Node.js or a browser. For Node.js use
$ npm test
or
$ node test/test
To test a single method, use, for example
$ node test/methods/toFraction
For the browser, open test/test.html.
Performance
See the README in the perf directory.
Build
For Node, if uglify-js is installed
npm install uglify-js -g
then
npm run build
will create bignumber.min.js.
A source map will also be created in the root directory.
Feedback
Open an issue, or email
Michael
Licence
The MIT Licence.
See LICENCE.